マルチメディア論および演習

音とは

音声波形

音は，ある物体の振動(往復運動)によって生じ，それが，空気の粗密状態(空気の密度，つまり大気圧，の微妙な高低のこと)の周期的な繰り返しとして周囲に伝播して伝えられる．人間の耳は，それをの鼓膜の振動運動として復元し，それを人間の脳が音として知覚する．

　

粗　　　密　　　粗　　　 密　　　 粗　　　密　　 粗
→時間
	↑密 ↓粗
→時間

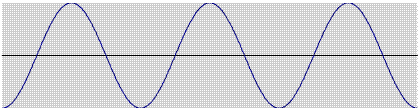
上の図は，空気の粗密を白黒の度合で表したものである．その図に示された空気の密度の高い・低いをそのまま縦軸としてグラフにしたものが，その下の図である．両者とも横軸は時間を表す．両方とも録音マイクの場所で空気の粗密が時間によってどのように移り変わっているかを示している．通常は，音データを示す音声波形として，下の方の図が一般的に用いられる．

音の3要素

ある音を特徴づけるには，次の3要素を考慮する．

• 振幅(amplitude)
• 周期(period)，周波数(frequency)
• 波形(waveform)

振幅は，上の図では波の高さに対応し，人間の聴覚には音の大きさとして知覚される．音の大きさは，音圧と呼ばれ単位はdb(デシベル)で表現される．

周期は，波の繰り返しにかかる時間のことであり，上の図では波の一周期分の横の長さに対応する．周波数は，1秒間に何回繰り返されたかを示し，周期をTとすると周波数f=1/Tとなり，実質的に波の繰り返しに関わる同じ性質を表す特徴である．周期の単位は時間の秒(sec)であり，周波数は1秒に1回繰り返されるものを1Hz(ヘルツ)とする．これらは人間の耳には音の高さに関係して知覚され，周波数の高い音(周期の短い音)は高い音，逆に周波数の低い音(周期の長い音)は低い音に聞こえる．ちなみに人間の耳で知覚できる可聴周波数は，16Hzから25,000Hz程度である．

波形は，人間の耳には音色や音質として知覚される．上の図に示したいわゆるsinカーブで示されるような，一番自然になめらかに高低が遷移する波形の音のことを純音(pure tone)と呼ぶ．純音の例としては音叉の音などがある．デジタル音声では鋸の歯のような角張った形の波形もよく利用される．

人間の会話や音楽など現実世界の音声波形

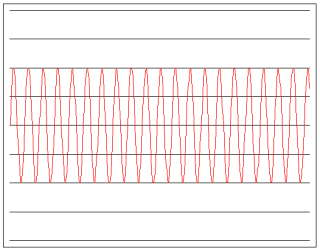
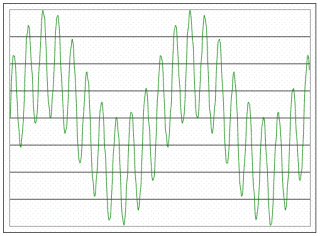
現実世界の音の多くは，もちろん純音だけではなくさまざまな周波数や波形が混ざった音である．わかりやすく周波数だけに着目して，次のような高周波の純音と低周波の純音があったとすると，その合成波形(ふたつの波形の同じ位置の値を単純に足し算したもの)は下の図のようなものになる．

+

						

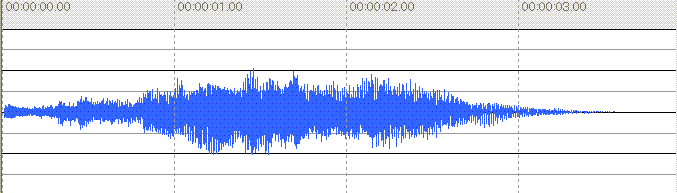
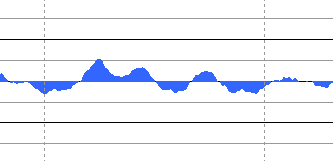
実際の人間の声や楽器の音などは，2つだけでなくたくさんの周波数成分の合成波形である．さらに，実際の会話や音楽を録音したデータでは時間とともに音そのものが変化する．例えば「こんにちは」という音声データであれば，時間とともに「こ」「ん」「に」「ち」「は」という五つの音を連続的に変化させた波形となる．実際の音声波形の例としてWindowsXpの起動音(c:\Windows\Media\startup.wav)の波形を図に示す．下はその波形の一部を拡大したものである．かなり複雑な波形に見えるが，複数の周波数の音を合成したことに変わりはない．

音声波形の周波数スペクトル

逆に，実際の音声波形からある特定の周波数の音がどの程度含まれているかを調べることを，周波数解析と呼ぶ．周波数を解析することで，不要な周波数成分だけを除去(例えば，録音した会話から雑音成分だけを除去)したり，音楽データから低音や高音など特定の周波数の音だけを増幅したり遮断する機能(イコライザー)を実現したりする，さまざまな音声波形の加工が可能となる．

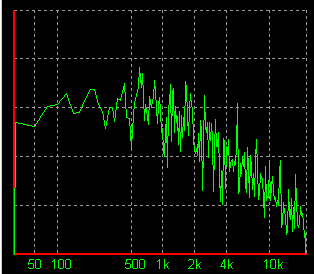
周波数解析の結果，周波数別にどの程度その音が含まれているかを示した分布のことを音の周波数スペクトル(spectrum)と呼ぶ．上のWindowsの起動音のほぼ中央あたりの一定区間だけ取り出したときの周波数スペクトルを図にしたものが，下の図である．

日本語ではspectrumはカタカナでスペクトルまたはスペクトラムと表記される．どちらでも構わないが，ひとつの文章中では統一しないと混乱するためこのテキストではスペクトルに統一する．

音声波形のデジタル化

デジタイズとは

音声波形のようなアナログ情報をデジタル化することをデジタイズ(digitize)と呼ぶ．特に音声信号をデジタイズする場合には，次の作業が必要となる．

• 標本化(sampling)，サンプリング
• 量子化(quantize)

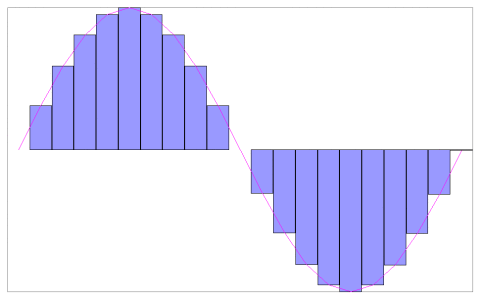
上の図の例では，ピンクの音声波形を青色の棒グラフに変換するデジタイズ作業を示している．標本化とは，時間を短い一定時間ごとに区切ってひとつひとつを読み取ることを示す．また量子化とは，読み取る波形の振幅値をデジタルデータとして切りのよい数字に切り上げたり切り下げたりすることをいう．横軸(時間軸)をいくつに分割するかを標本数，分割する時間の幅を標本周期，その周波数を標本化周波数あるいはサンプリングレート(sampling rate)と呼ぶ．また，棒グラフの高さの段階数のことを量子化サイズ(sample number)と呼び，量子化サイズが表現するのに十分なビット数(2ⁿで表現したときのnのこと)を量子化ビット数と呼ぶ．十分に標本周波数が高く量子化ビットが大きければ，この棒グラフは元の波形を良く近似することができる．

サンプリング定理(標本化定理)

このデジタイズに対する重要な定理として，サンプリング定理がある．これはナイキスト(H.Nyquist)が1928年に発見し，その後1949年にシャノン(C.E.Shannon)と染谷勲が数学的証明をそれぞれ独立に行った．このため「シャノン・染谷の標本化定理」「シャノンの標本化定理」と呼ばれることもある．

サンプリング定理:

入力波形に含まれる最大の周波数成分をWとしたとき，標本化周波数が2W以上であれば，標本化されたデータから元の入力波形を「完全に」再構成できる．

この周波数2Wのことを，ナイキスト周波数と呼ぶ．

この定理は，ある波形からとびとびの標本値を取得して，その標本値を順番どおりに間をつなぐ作業(補間と呼ぶ)をおこなうことで，元の波形を完全に再構成することを意味する．逆にいえば，ある波形に標本化周波数の2倍以上の周波数成分が含まれていた場合には，正確に音を再現できないことを示す．その場合，Wよりも低い音の成分として再現されてしまい，エイリアスと呼ばれ，ノイズの原因となる．

実際に利用されているデジタイズ品質

音声をデジタル化するにも，文字同様にいろいろな方法があり，目的に応じて選択される．例えば音響・音楽目的ならば，音声の再現性に重点をおいた方法でデジタルデータにしなければならない．しかし電話などの音声目的ならば，音の再現性よりも通信のための圧縮率を重視しなければならない．その観点で実際に標本化周波数や量子化ビット数を決定する必要がある．

目的	量子化サイズ	サンプリングレート
電話のデジタル回線	8bit	8kHz
CD	16bit	44.1kHz
DAT	16bit	48kHz
DVD-Video	24bit	96kHz(最大)
DVD-Audio	24bit	192kHz(最大)
BD/HD-DVD	24bit	192kHz(最大)

人間の声は，およそ100Hzから8000Hzの範囲におさまるといわれる．さらに会話を聞き取れる程度にまでしぼれば，300〜3400Hz程度あれば十分である．このため電話では，その2倍の周波数にさらに余裕を見て8kHzでサンプリングされて伝送される．また，すべての楽器の音を含めるためには，人間の可聴周波数領域全体を録音する必要があるため，CDでは人間の可聴周波数の上限を20kHzとして44.1kHzが採用された．しかし，その後人間の可聴周波数はもっと高いのではないかとの議論があり，その後の規格では徐々に引き上げられ，現在最高品質のデジタル音声の媒体であるDVD-Audioでは最大192kHzのサンプリングレートを利用することができる．さすがにそれ以上は人間の聴覚の性能を明らかに越えるため，次世代DVDでも同じ品質である．