第4回
目標
- 待ち行列のシミュレーション
- 待ち行列の考察
待ち行列のシミュレーション
待ち行列理論とは
はじめに,ファストフードのカウンターを考えてみよう.お客は開店時間から次々と到来し,カウンターでハンバーガーやドリンクなどの注文する.1人のお客の注文を店員が対応している間にも別のお客が到着するので,カウンターには行列ができる.これを「待ち行列」と呼ぶ.
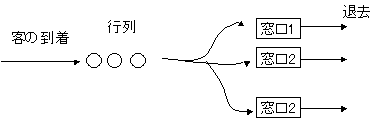
図1 待ち行列モデル
待ち行列の長さや待ち時間は,店員の処理能力やお客がどれくらいやってくるかに依存する.通常,カウンターでの一人あたりの対応時間の長さ(平均処理時間)は,どれくらいの時間間隔で客がやってくるか(平均到着率)よりも短くなければならない.そうでなければ,行列は増える一方でありその店は破綻してしまう.この場合わざわざ理論を立てるまでもない.
しかし,仮に対応時間が十分短かったとしても行列はできる.平均はあくまで平均であり,一度にたくさんのお客が押し寄せる瞬間もあるし,たまたま注文の品に時間がかかってしまって次の客を待たせてしまうこともある.(もちろん,逆にまったくお客がこない時間帯もあるはずだ.) つまり,このように客の到着や注文の品の処理にかかる時間などにばらつきがあるために(確率的なゆらぎのために),対応時間が十分短い場合でも,待ち行列は発生する.
このような対応時間が十分短い場合に発生するような待ち行列で,その行列の長さの平均や待ち時間の平均など,振待ち行列の振る舞いを知るために,解析的に解いた理論が待ち行列理論である.
待ち行列理論を使うと,行列を長くしないようにするために,カウンター窓口の数を増やすべきか,あるいはサービスにかける時間を短くするか,それによってどれほどコストがかかるのかなどを判断できるようになる.ファストフード店の例だけでなく,カウンターの代わりに工作機械,客の代わりに加工したい部品の素材と考えれば,工場で工作機械の数を増やすかどうかの判断なども,まったく同じ待ち行列理論で対応できる.
しかし現実的な待ち行列の状況を数学的に解くことはきわめて難解である.たとえば,行列の長さがある程度以上になると帰ってしまう客がいたり,少しでも行列があると他の店に客が流れてしまったり,なども考えられる.そこでシミュレーションを使い,机上で試行を繰り返すことで解答を得ることが可能になる.
待ち行列のモデル
まずは待ち行列のモデルを設定する.待ち行列モデルを用意する場合,決めなければならないことは客の到着間隔と,客1人あたりに必要なサービス時間である.待ち行列モデルの典型例では,一定時間内の客の到着数をポアソン分布だと想定する.例えば,平均が3のポアソン分布は次のようなものである.
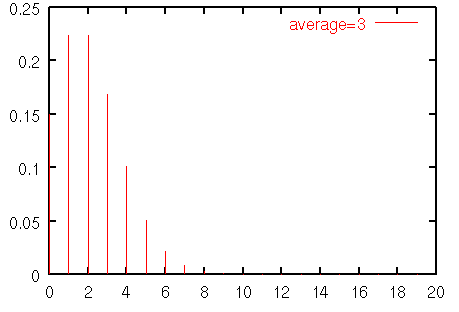
図2 平均3のポアソン分布
ポアソン分布は,離散分布であり,整数値だけをとる.
またサービス時間は指数分布に従うとされる.次のような連続分布である.

図2 指数分布関数
実はポアソン分布と指数分布は表裏一体であり,指数分布に従った時間間隔で客が到着すると,単位時間あたりの到着数はポアソン分布になる.ただし,逆は厳密の意味では成り立たない.ポアソン分布は離散分布であり,整数値しか取らないため,それを使って指数分布などの連続分布を作り出すことはできないからである.
これら分布の具体的な確率密度関数など数学的背景についてはここでは触れない.
このように,到着がポアソン分布,サービス時間が指数分布に従い,窓口がひとつだけのモデルをケンドールの記号を用い,M/M/1モデルと表現する.Mがポアソン分布あるいは指数分布を表す.他に,
- D: 単位分布 (定数)
- G: 一般分布
- E: アーラン分布
などがある.例えば,到着が一般分布,サービス時間が単位分布,窓口が3つの場合,G/D/3と表現する.
M/M/1モデルが待ち行列モデルの典型例である.M/M/1モデルを確率の面から考えて,解析的に解くと,
- 平均到着率(単位時間あたりの客の到着数)をλ
- 平均サービス率(単位時間あたりの処理数)をμとしたとき
- 系平均待ち時間(自分のサービス時間を含む) は 1/(μ-λ)
- 列平均待ち時間(自分のサービス時間を含まない)は λ/μ(μ-λ)
- 系平均人数(自分のサービス時間を含む,平均待ち行列の長さ)は λ/(μ-λ)
- 列平均人数(自分のサービス時間を含まない待ち行列の長さ)は λ*λ/μ(μ-λ)
となることがわかっている.
モンテカルロシミュレーションによる待ち行列の解
この待ち行列の振る舞いをシミュレーションするには,客の到着間隔と,サービス時間を,発生させた乱数によって決定する.単純なM/M/1モデルの場合,両者とも指数分布に従う乱数を発生することが考えられる.あるいは,単位時間あたりの客の到着人数と,単位時間あたりのサービス人数をポアソン分布に従った乱数によって決定することも考えられる.ここでは時間間隔の方を乱数で発生させるシミュレーションを行うことにする.
指数分布に従う乱数を発生させるには,表計算ソフトで次の式を用いればよい.(Excelの分析ツールにある乱数の発生ツールでは,指数分布に従う乱数は発生できない.ポアソン分布は発生できる.) 一様分布の乱数をrand()で生成し,次のように変換する.
- r = -n * ln (1 - rand())
ここで,nは発生させる乱数の平均値である.
指数分布に従う乱数を2組発生し,それぞれ客の到着間隔と,サービスに要する処理時間と考える.それらを累積したりしながら次のようなシミュレーションを作成できる.図4で特に注意すべき項目は,処理開始時刻である.到着時刻より前に開始できないのは当然のことであるが,前の人が終了しなければ開始できない点に注意すること.
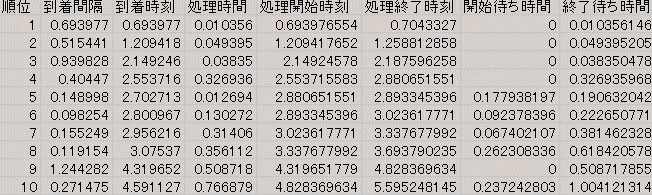
図4 シミュレーションシート
この図から,開始待ち時間の平均および終了待ち時間の平均を求めて,系平均待ち時間,列平均待ち時間を求めることができる.また,この開始待ち時間の合計を全員の処理を開始するまでに要した時間,すなわち最後の人の処理開始時刻で除したものが,列平均待ち行列の長さになる.系平均待ち行列の長さの方は,同様に終了待ち時間の合計を最後の人の処理終了時刻で除したものである.
