第2回
目標
- Windows上でExcelの使用
- モンテカルロシミュレーション
- レポートの書き方
Windows上でのExcelの使用
4-108教室でWindowsを起動するには,最初のメニューで「Windows」を選択すればよい.ユーザ名とパスワードは次のように入力する.
- ユーザ名: nit?? (??には席番号)
- パスワード: 授業中に指示
表計算ソフトExcelは次のようにWindowsメニューから選択して起動する.
- アプリケーション→Microsoft Office→Microsoft Office Excel
Excel2003の基本的使用方法は春学期使用したOpenOfficeCalcと類似している.ただしいくつかメニュー項目の中身が異なるため,必要な機能が見つからないときには落ち着いてメニュー内をよく探し出すこと.
モンテカルロシミュレーション
シミュレーション(simulation)とは
シミュレーションという言葉自体は,現在皆聞いたことはある言葉であろう.(注:「シュミレーション」 と間違えている人が時々いるが,とても恥ずかしい)
もともとの英語では,「…の真似をする」という意味から,現在のコンピュータ分野では軍事・経済・政治・物理など様々な現象にたいしてモデルを構築し,コンピュータによる模擬実験を行い,状況変化や結果を予測することを指す言葉となった.
通常は,理論式がわからない,あるいは理論式があっても複雑すぎて解くことができないような自然現象一般に対して,その現象をどうしても解きたいときにシミュレーション手法を用いる.例えば,ビル崩壊のメカニズムの解析など,複雑な物理現象がどのように発生したかを推測するために用いたりする.
シミュレーションといえども,対象とする現象を正しく真似できなければ,間違った答を導いてしまう.シミュレーションを行う際には,シミュレーションに用いる入力が適切か,その入力を処理するモデルが適切か,十分検討する必要がある.

図1 入力→変換(モデル)→出力
モンテカルロ法とシステマティック法
シミュレーション手法は,大きくモンテカルロシミュレーションとシステマティックシミュレーションに分けることができる.他にも数値シミュレーションか非数値シミュレーションかなどいくつか分類の切り口があり,また実際に用いられる手法はこれらを巧みに組み合わせて使うことも多い.ある手法を単純に分類することはできない場合もある.
シミュレーション手法の中でも特に有名なモンテカルロ法とは,シミュレーション対象の現象に対して,その入力に大量の乱数を十分与えて出力値を観測することで,その現象を確率的に解いてみる手法である.乱数を用いることから,賭け事の街として有名なモナコの都市モンテカルロの名がつけられた.乱数は,シミュレーション対象の自然現象への入力として最もふさわしい確率分布,例えば一様分布など,に従う必要がある.
それに対してシステマティック法では,乱数は使わずに,決定的に(ただ一回の計算で)解を求める.
例 円周率を求める
モンテカルロシミュレーションの説明によく使われる例として,円周率の計算がある.

図2 円と正方形の面積比
円の面積はπ×r×rである.その円に外接する正方形の面積は4×r×rである.ここで正方形の面積を基準としてこの円との面積比をaとすると a = (π×r×r)/(4×r×r)となる.この式を変形すると,
π=4×a
のような式が得られる.つまり,なんとかしてaの値さえ推定できれば,この式から円周率を推定できる.
モンテカルロ法を使ってaの推定を行う場合は,次のように考える.
図2のランダム(でたらめ)な場所に点をたくさん打つとする.例えば全部でN個の点を打ったとして,その中で円の中に打たれた点の数を数える.これをnとする.Nを十分大きくしていけばnとNの比は,円と正方形の面積の比に近づくはずである.つまりあるNに対して実際にnの値を測定することで
a = n/N
としてaを推定することができる.
####################
余談
一方,システマティック法の場合は,次のように考える.モンテカルロ法と異なり,乱数を用いない.この場合は,ランダムな位置に点を打つのではなく,正方形の中をきっちり格子上にわけて,点を打つ.つまりN個の点を打つ場合は,1辺を√N個に分けて桝目を作る.あとはモンテカルロ法の場合と同様に,円内の点の数を数え,面積比n/Nを計算する.
余談ここまで
#####################
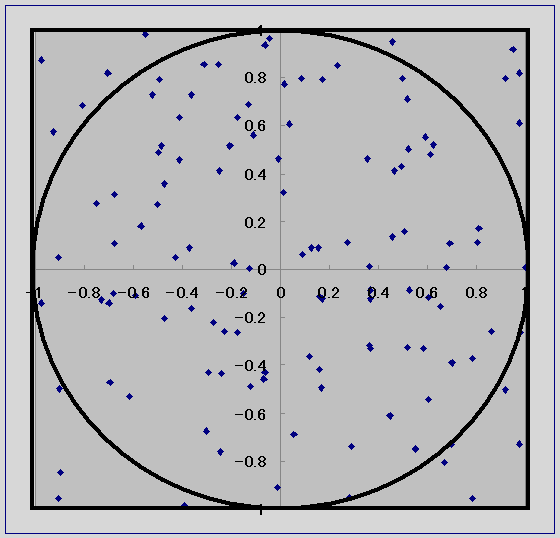
図3 モンテカルロシミュレーションによる円と正方形の面積比の求め方
